Menu

Office Camera

There is a webcam in my office that I use to take photos of the whiteboard. This setup was inspired by Dror Bar Natan’s Blackboard Shots. You can read more about the setup here. If you know of anyone else with a similar setup, please let me know.

This page generates an RSS Feed.

• ««
• «
• 13
• 14
• 15
• 16
• 17
• »
• »»

Matrices and Transformations

Diagonalization of 2x2

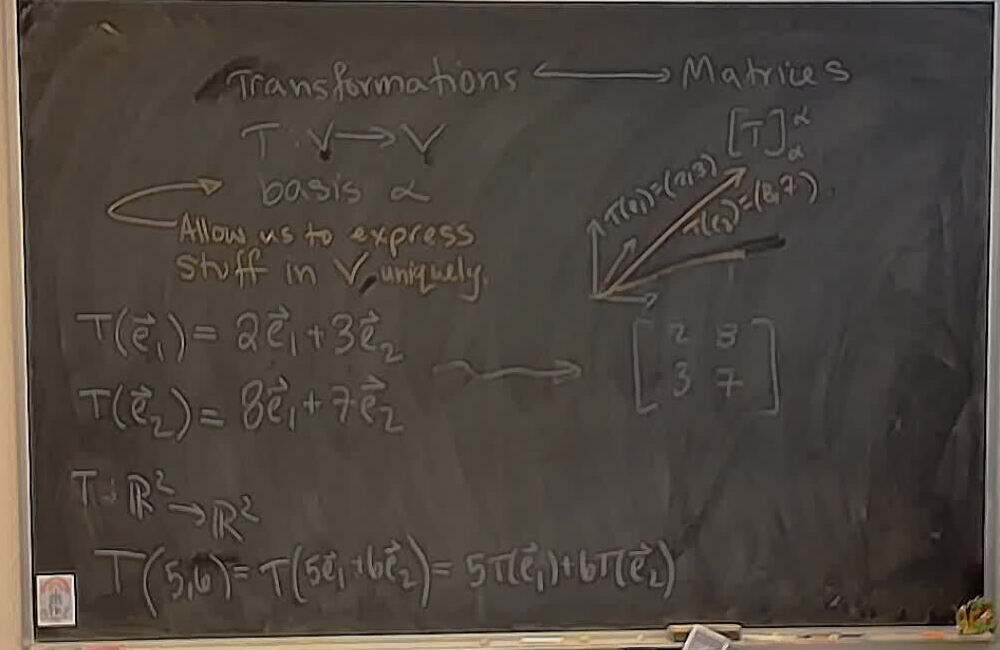
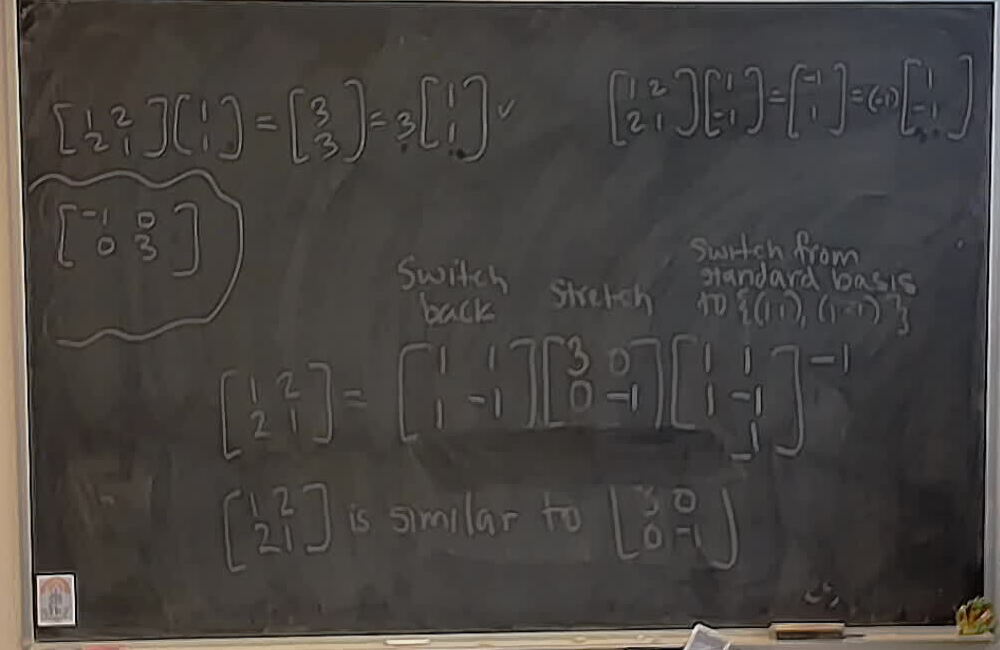
Diagonalizing the matrix: \[ \begin{bmatrix} 1 & 2\ 2 & 1 \end{bmatrix} \]

Equitorial Dial: Step 1

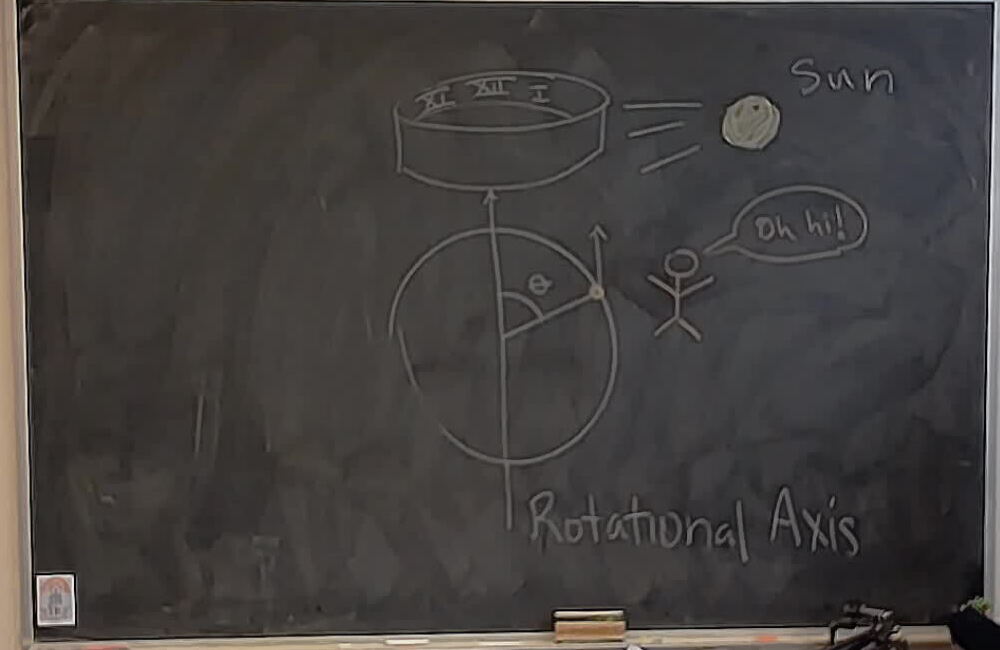
A sketch for a piece about sundials. This shows the first step in designing an equitorial dial.

2025-03-26 @ 11:52:04

B42 TT1 Q4

Generalized Stokes Theorem on A Box (Part 2)

Generalized Stokes Theorem on A Box (Part 1)

MAT B42: HW 2 Q 2

MAT B42: HW 4 Q 3

Sundials and Equinoxes

Navigation Menu

Home / Now / Blog / Notes / Reading / Office Camera / Tags / Bookmarks / RSS Feeds / Top of Page

Thanks for reading! If you have any comments or questions about the content, please let me know. Anyone can contact me by email.